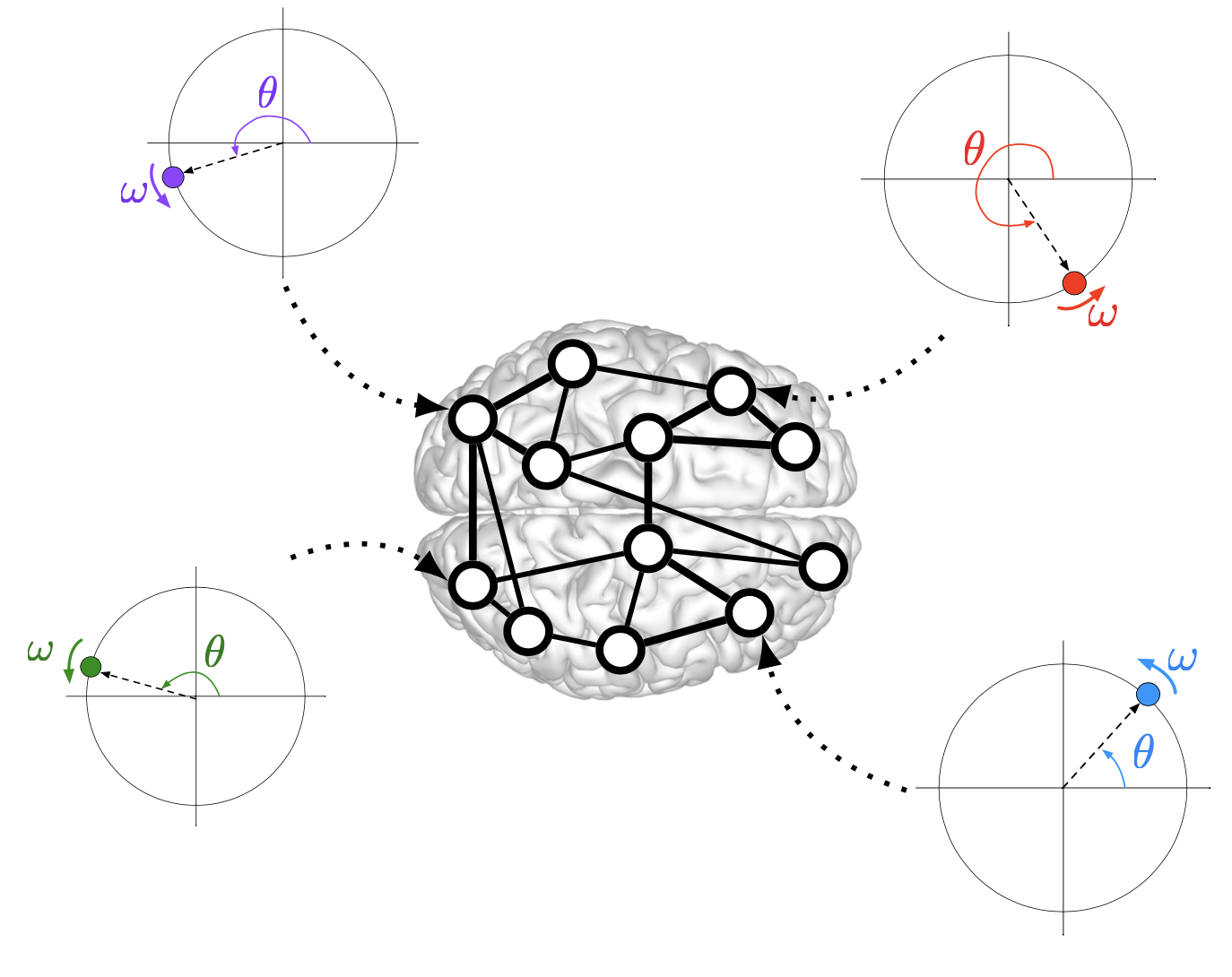
Synchronous neural activity enables a multitude of functions in the brain. Examples include motor coordination, sleep spindles, circadian rhythms, and large scale integration of sensori stimuli. Furthermore, synchronization can be used as a biomarker in multiple neurological disorders, and abnormal or decreased synchronized activity has been linked to neurological damage or cognitive decline due to aging. Yet, a complete characterization of synchronization phenomena in the brain is far from complete. By studying the brain as a complex dynamical system of interconnected neural populations, we contributed towards the theoretical understanding of the synchronization of interconnected brain regions. Specifically, by abstracting oscillatory neural populations as nonlinear oscillators, we revealed the mechanisms that enable a variety of synchronization phenomena in groups of oscillators.
For more details see, for instance:

1. Our Nature Communications paper Functional Control of Oscillator Networks

2. The works Stability Conditions for Cluster Synchronization in Networks of Heterogeneous Kuramoto Oscillators, A Framework to Control Functional Connectivity in the Human Brain, Exact and Approximate Stability Conditions for Cluster Synchronization of Kuramoto Oscillators, Relay Interactions Enable Remote Synchronization in Networks of Phase Oscillators
   

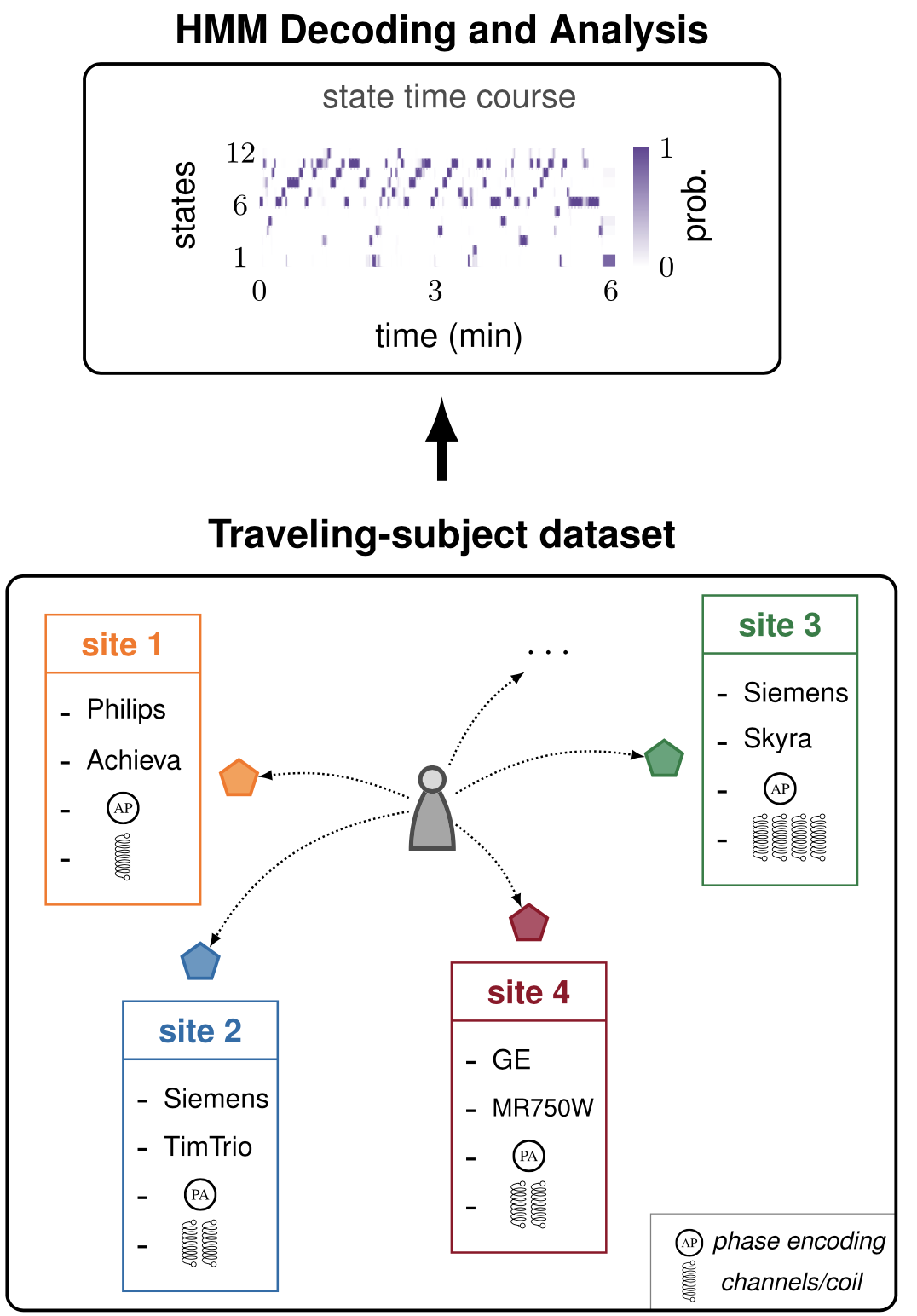
Large multi-site neuroimaging datasets have significantly advanced our quest to understand brain-behavior relationships and to develop biomarkers of psychiatric and neurodegenerative disorders. Yet, such data collections come at a cost, as the inevitable differences across samples may lead to biased or erroneous conclusions. In this line of work, we aimed to validate the estimation of individual brain network dynamics fingerprints and appraised sources of variability in large resting-state fMRI datasets by providing a novel point of view based on data-driven dynamical models. Specifically, we utilized hidden Markov models to examine how diverse scanning factors in multi-site fMRI recordings affect our ability to infer the brain's spatiotemporal wandering between networks of activity.
For more details see our work Brain Network Dynamics Fingerprints are Resilient to Data Heterogeneity

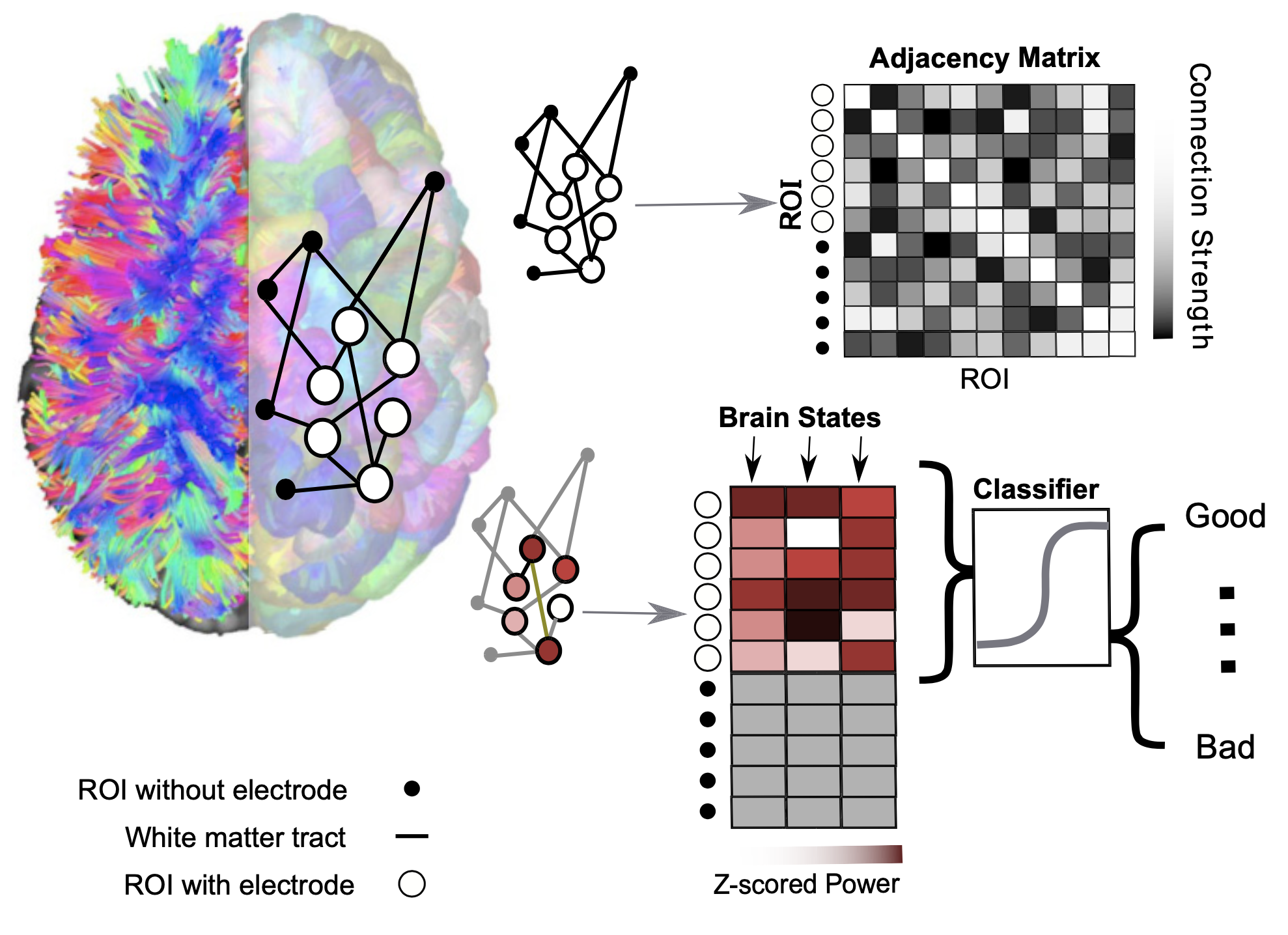
The brain can be studied as a network system in which nodes represent brain regions and the links connecting these regions are defined by white matter tracts. We used optimal control theory – finding control laws for a given system such that a certain optimality criterion is achieved – to predict and analyze multiple memory states from an energetic point of view. Our work quantified the role that the anatomical organization of the brain plays in constraining its dynamical response to external current stimulation. As a proof of concept, we tested which brain states and structural properties will efficiently improve memory encoding when stimulated. Furthermore, we also found that subjects affected by schizophrenia show diminished stability of minimum-energy working memory states.
Related publications: White Matter Network Architecture Guides Direct Electrical Stimulation Through Optimal State Transitions, Brain network dynamics during working memory are modulated by dopamine and diminished in schizophrenia

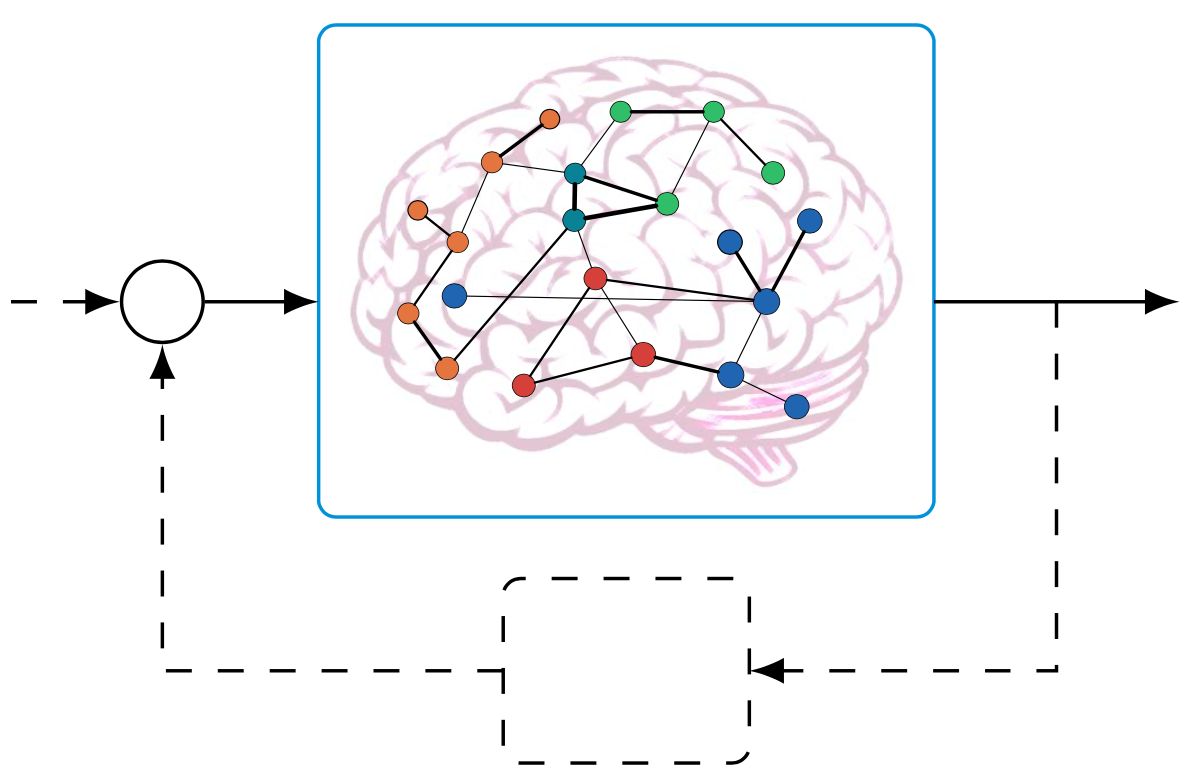
The intersection between control theory and the study of the brain as a network system has the potential to overhaul our understanding of the brain dynamical wandering between different states. The possibility to steer the state of a network system through endogenous or exogenous stimuli – controllability – is determined by the network organization. By employing control-theoretic tools, we (i) provided prescriptive conditions for structural brain networks to be theoretically controllable, (ii) characterized the features that enable the simplification of nonlinear network systems, and (iii) demonstrated that structural brain networks possess distinct controllability profiles with respect to random networks. These methods and tools holds the promise to inform the development of novel treatments and stimulation schemes to treat multiple neurological disorders.
Related publications: Conditions for Feedback Linearization of Network Systems, Structural Controllability of Symmetric Networks, The Structured Controllability Radius of Symmetric (Brain) Networks